Приведем решение уравнения (1) xⁿ + yⁿ = zⁿ к решению уравнения прямоугольного треугольника, для чего построим фигуру согласно рис. 4.

Рис. 4.

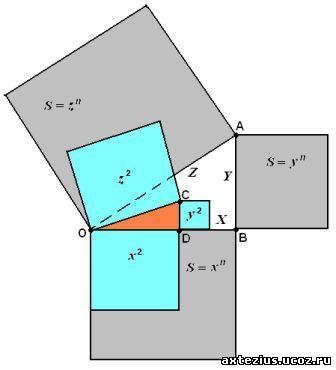
На сторонах прямоугольного треугольника построим квадраты с площадями xⁿ; yⁿ; zⁿ, где n > 2 и стороны которого будут равны: X = √xⁿ; Y = √yⁿ;

Z = √zⁿ. В данный треугольник впишем гипотетический треугольник со сторонами x; y; z, предположив, что он так же является прямоугольным.

Приведем уравнение (1) к виду:

         x^n-2x² + y^n-2y² = z^n-2z²    или  Ax² + By² = Cz² (10),

      где: A = x^n-2;  B = y^n-2;  C = z^n-2;  а квадраты x²; y²; z² есть единичные квадраты (на рис. 4 – квадраты голубого цвета).

Исходя из указанных выше закономерностей существования пифагоровых чисел, следует, что если для какого-либо значения n существует решение в натуральных числах, то должно быть соблюдено равенство:

    (mx² + my² = mz²) = (Ax² + By² =Cz²)

Т. е. должно быть соблюдено равенство A = B = C = m.

Исследуем этот вопрос:

 В уравнение (10) вместо x и z подставим их значения согласно уравнениям (5), (6), которые являются единственно истинными для решения прямоугольного треугольника. Кроме того, уравнение (5) разрешает неопределенность квадратного уравнения (3) тем, что графиком его является парабола, на ветвях которой отражены значения как (x – yi), так и (x + yi).

  Получаем уравнение:             

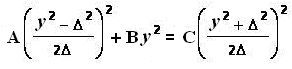
  После возведения в степень и сокращений получим:

    Ay⁴ + 2Ay²²+ A⁴  + 4By²²  = Cy⁴ + 2Cy²² + C⁴;           y⁴(A - C) + 2y²²( 2B - C - A ) +  ⁴( A - C) = 0

     ( A - C) (y⁴ + ⁴ ) + 2y²²(2B - C - A) = 0

  ( A - C) (y⁴ + ⁴ ) = -2y²²(2B - C - A)

          Таким  образом, данное уравнение имеет  решение относительно коэффициентов, только когда:                                  Возьмем:            

        ( A - C) =  -(2B - C - A)  откуда:   B = C. 

             (A – C) = 0;    откуда:      A = C.

    Возьмем:             (2B – A – C) = 0;   откуда: 

Это следует понимать так, если мы имеем квадрат площадью zⁿ и  стороной, выраженной натуральным числом, то его можно разложить только на один квадрат площадью xⁿ  или  yⁿ со стороной выраженной натуральным числом. Сторона второго квадрата никогда натуральным числом выражена не будет.                                                                 

И обратный вывод, если сложить два квадрата площадями  xⁿ  и  yⁿ, то сторона суммированного квадрата никогда не будет выражена натуральным числом. Следовательно, решение уравнения  zⁿ = xⁿ + yⁿ для любых n > 2, не существует.

Но придти к данному доказательству возможно только после детального изучения свойств пифагоровых чисел, а это возможно было сделать только методом Пифагора, т. е. используя уравнение (5).

P.S.  Вопрос: Достаточно ли было П. Ферма данного доказательства для вывода своей Великой теоремы?