Никита Акс.
Логический анализ учения Пифагора.

О жизни Пифагора, его учении и учениках уже столько написано и сочинено, что мне добавить нечего. А вот проанализировать достоверно дошедшие факты, меня подвергла работа над «Диалектикой чисел».
Начинаю с цитат из Википедии:
1. Согласно традиции, последователи Пифагора делились на акусматиков
(«слушателей») и математиков («учеников»). Акусматики имели дело с религиозными и ритуальными сторонами учения, математики — с исследованиями четырёх пифагорейских «матем»: арифметики, геометрии, гармоники и сферики. Акусматики не считали математиков «настоящими пифагорейцами», но говорили, что они ведут своё начало от Гиппия, изменившего исходной пифагорейской традиции, раскрывшего тайны непосвящённым и начавшим преподавание за плату.
2. Из геометрических работ пифагорейцев на первом месте стоит знаменитая Пифагорова теорема. Доказательство теоремы должно было явиться результатом потребовавших значительного промежутка времени работ, как самого Пифагора, так и других математиков его школы, начавшихся на арифметической почве. Член ряда нечётных чисел, всегда являющийся разностью между двумя соответствующими членами ряда квадратных чисел, мог быть сам числом квадратным: 9 = 25 — 16, 25 = 169 — 144, … Содержание пифагоровой теоремы было, таким образом, впервые обнаружено рациональными прямоугольными треугольниками с катетом, выражаемым нечётным числом. Вместе с тем должен был раскрыться и Пифагоров способ образования этих треугольников, или их формула (n — нечетное число, выражающее меньший катет;
(n2 — 1)/2 — больший катет; (n2 — 1)/2 + 1 — гипотенуза). Вопрос о подобном свойстве также и других прямоугольных треугольников требовал соизмерения их сторон. При этом пифагорейцам впервые приходилось встретиться с несоизмеримыми линиями. До нас не дошло никаких указаний ни на первоначальное общее доказательство, ни на путь, которым оно было найдено. По свидетельству Прокла, это первоначальное доказательство было труднее находящегося в «Началах» Евклида и также основывалось на сравнении площадей.
NB! Здесь я хочу особо выделить, что Пифагор не признавал иррациональные числа, он занимался исследованием только рациональных чисел и, в первую очередь - натуральных. А так же должен был заниматься изучением пропорций образованных отношениями сторон прямоугольных треугольников .
Из этого следует, что Прокл не знал, как Пифагор пришел к выводу указанных уравнений и, исходя из того, что теорема Пифагора и доказательство Евклида основаны на сравнении площадей и сторон треугольников, сделал вывод, что и эти уравнения выведены аналогичным способом. При этом ввиду отсутствия доказательства сделал вывод, что данное доказательство, значительно сложнее доказательства Евклида.
Так каким же способом Пифагор нашел эти уравнения? Сколько я не бился с нахождением данного решения жонглированием треугольников, ничего не получилось, а потому считаю, что единственно логически простой и к тому же наиболее элементарный метод заключался в следующем: На радиус окружности вписываем прямоугольный треугольник ОАВ
(см. рис. 1), при этом радиус окружности равен Z, а так же равен
(X + Δ).
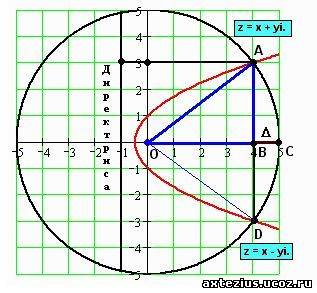
Если же данный рисунок отобразить в прямоугольных координатах (см. рис. 2), то полученный чертеж иллюстрирует не только свойства многих геометрических фигур, но и комплексные числа.
Рис. 1.
В дальнейшем, выделенное уравнение буду называть:
Пифагоровым уравнением.
Рис. 2.
Теперь, найдя основное уравнение решения прямоугольного треугольника в натуральных числах, естественно, Пифагор установил зависимость шага возрастания значений Y, от значений Δ. Теперь он получил возможность детального изучения Δ- функций. Следуя логике любого исследования и психологии исследователя, Пифагор должен был объединить функции Δ = 1 и Δ = 2 по порядку чередования значений Y (четное – нечетное). Естественно, при этом он должен был увидеть, что разность между соседними значениями X всегда равна квадрату натурального числа. И, разделив функцию Δ = 2, по значениям X, на четную и нечетную гармонику, составить алгоритм триединства. Открыв все это, Пифагор понял, что открыл нечто фундаментальное. Он не знал законов колебания маятника, но, составляя таблицы троек, согласно значениям Δ, определил, что все значения X, Y, Z, а также свойства дельта функций напрямую зависят от значения Δ. Но значения дельта ни с чем и никак не связаны, они являются самостоятельной величиной. Поэтому Пифагор определил Δ, как Бога. Отсюда и определение, пришедшее к нам от его учеников: все числа от Бога; Бог явлен в числах.
И именно об алгоритме триединства он говорил своим ученикам, не открывая при этом его тайну. Впоследствии, не зная алгоритма триединства, многие его последователи и исследователи посчитали, что это алгоритм «золотого сечения». Но «золотое сечение» всегда выражено рациональным (дробным) числом, а Пифагор эти числа не признавал. А не признавал он их потому, что и Δ- функции и алгоритм триединства всегда выражены натуральными числами.
Продолжая исследования открытых им функций, Пифагор не мог не обратить внимания на чередование последних цифр в значениях X, (знаю по собственному опыту). Тем более это будет заметно при буквенном написании цифр. Естественно, что при этом он сделал то же, что в свое время сделал и я, просто из любопытства. А именно, заменил числа суммой их цифр в однозначном счислении и, тем самым открыл, что числа являются, в своей основе, гармоническими колебаниями, установив при этом, что каждой Δ- функции соответствует своя формула волны. Справедливость этого доказывается элементарным графиком отображения формулы волны любой Δ- функции:
Что же он сделал дальше? Из отчета Гауденция следует:
«Он натянул струну на линейку и разделил ее на 12 частей. После этого он заставил звучать сначала всю струну, а затем ее половину, т. е. 6 частей, и нашел, что вся струна была в консонансе со своей половиной, причем музыкальный интервал представлял октаву. После того же, как он заставил сначала звучать всю струну, а затем 3/4 ее, он услышал консонанс кварты, и аналогично для квинты».
Так Пифагор приступил к изучению гармонических колебаний имитируемых числами, заложив основы нотной грамоты и введя понятия «гармония сфер» и гармонии чисел.
Примечание: Если предположить, что во время своего обучения у египетских жрецов, Пифагор читал «Книгу Еноха», что вполне допустимо, то совпадение периодов числовых колебаний, с периодом колебаний, указанных в Книге, его окончательно убедило в том, что числа происходят от Бога. Кроме того, я считаю, что когда Пифагор открыл свое уравнение, то он не стал его раскрывать жрецам, а как патриот своей родины, вернулся в Грецию, где продолжил свою работу и открыл свою Школу. В дальнейшем, его ученики и последователи пользовались переданными Пифагором знаниями, не понимая их сути, поскольку не был известен сам источник этих знаний.
Вот такой следует вывод, основанный на анализе самих пифагоровых чисел.
Колебания, имитируемые числами, в дальнейшем буду называть:
логосными колебаниями.
Вторым, кто проник в тайну уравнения X2 + Y2 = Z2, был Пьер де Ферма.
Но и он, из-за алгоритма триединства был лишен возможности опубликовать свою работу. Зато он оставил после себя знаменитую Великую теорему, на протяжении более трех столетий, привлекающую к себе внимание математиков, физиков и вообще всех любителей познавать непознанное.
Ну, а поскольку Бог любит троицу, то (по абсолютно мне непонятной причине), я стал третьим, кто проник в тайну этого фундаментального уравнения.
Я считаю, что на настоящее время есть только два основных уравнения для познания нашего Мироздания:
X2 + Y2 = Z2; и E = mc2.
В качестве эпилога: Всем, кто пожелает разобраться в этом более подробно – читайте и скачивайте «Диалектику чисел".
| 


